MA i EMA

W poprzednim odcinku tej serii przyjrzeliśmy się RSI jako wskaźnikowi „temperatury” waloru i co z niego można wyczytać. Dzisiaj notka o średnich kroczących. Rzecz w sumie jest prosta i trochę może niepoważnie wykładać kawę na ławę. Ale dla pełnego obrazu, na wszelki wypadek, odnotujmy przynajmniej ich obecność, jako że przydadzą się w wielu innych miejscach.

Średnia arytmetyczna to jak wiadomo suma kilku wielkości, podzielona przez ich liczbę. Mając na przykład ceny zamknięcia srebra (które jakoś się nam specjalnie podoba w roli przykładu) z ostatnich pięciu dni handlowych: pM, pM-1, pM-2, pM-3, pM-4 średnia cena będzie:

Skąd ten symbol MA? Ponieważ mamy dobę globalizacji i we wzorkach trzymamy się terminologii angielskiej. MA (moving average) oznacza wprawdzie to samo co średnia krocząca ale wygląda za to dużo bardziej naukowo. Ma też tę przewagę że z internetem pod każdą strzechą i w każdym obejściu na poj. Drawskim dużo łatwiej spotkać się teraz z MA niż ze średnią, a w dodatku kroczącą. 🙂

Ok. Sympatyczną cechą MA jest to że mając jej poprzednią wartość nie musimy za każdym razem wszystkiego od nowa dodawać. Wystarczy dodać do niej najnowszą cenę waloru podzieloną przez n oraz odjąć najstarszą cenę, również podzieloną przez n. Czyli

MAdziś = MAwczoraj – (pM-n+1 /n) + (pM+1 /n)

Pożytecznym zastosowaniem średnich kroczących jest wygładzanie grafików, w szczególności grafiku ceny jakiegoś waloru. Ruchy cen mogą być bardziej lub mniej gwałtowne, w tym wykazujące nieciągłości. W takich przypadkach nałożenie średniej kroczącej na grafik pozwala na lepsze zorientowanie się w trendach krótko- , średnio i długoterminowych. Na przykład, trzy średnie kroczące nałożone na grafik ceny spot srebra pokazuje poniższy diagram.

Widzimy tu niebieską linię odpowiadającą MA(12), czyli średniej kroczącej obejmujacej 12 dni (handlowych). Zgodnie z oczekiwaniami, linia ta w miarę ściśle pokrywa się z dziennymi zmianami ceny. Czerwona MA(50) jest średnią średnioterminową, i wykazuje dużo mniejsze wahania. W zasadzie mówi nam ona że mimo lokalnych panik tu i ówdzie srebro jest w 2007 w stabilnym trendzie wznoszącym. Długoterminowa średnia MA(200) (linia zielona) obejmująca 200 dni jest jeszcze bardziej łagodna, wykazując jedynie lekkie opóźnienie w okolicach przełomu roku i lekkie przyspieszenie +/- obecnie. Specjalnie ciekawe rzeczy wynikają z wzajemniej interakcji dwu MAs o różnym zakresie. Zwrócimy na to uwagę w kolejnym odcinku tego cyklu.

Problem z MA jest jej bezwładność. Coś mniej więcej tak jak z bankiem centralnym i inflacją… Zanim bank centralny się kapnie że przeholował z drukowaniem pieniądza, może już widzieć za oknem wzburzone masy palące kukły prezesa… :-).

Podobnie z MA. Czasem zdarza się że walor dozna gwałtownej przeceny, czy też gwałtownie poszybuje w górę w przeciągu dnia. MA jednak zauważa to dopiero po jakims czasie, przy czym tym dłuższym im dłuższy jest jej zakres. W diagramie powyżej widzimy na przykład że na korektę z początków marca niebieska MA(12) zareagowała w miarę szybko, natomiast MA(50) i MA(200) jej prawie nie zauważyły.

Pomysłem na „uczulenie” MA jest przypisanie różnych wag poszczególnym jej składnikom. W odróżnieniu od wzorku [1] gdzie każdy składnik miał wagę 1 w tym przypadku każdy składnik będzie miał inną. Na przykład, dla MA(5) możemy wziąć ostatnią wartość i pomnożyć ją przez 5, przedostatnią, jako mniej ważną, pomnożyć przez 4, kolejne wstecz przez 3, 2 i wreszcie najstarszą wartość pomnożyć przez 1 czyli zostawić w spokoju. Całość musimy jeszcze podzielić, teraz nie przez n a przez sumę naszych wag, a więc przez n + (n-1) + (n-2) + … +1. Mamy więc coś takiego:

gdzie n jest liczbą wartości wziętych do naszej średniej a WMA (weighted moving average) oznacza ważoną średnią kroczącą. Nasze wagi 5,4,3,… przydzielone poszczególnym wartościom zmiejszają się w tym przypadku liniowo, tak jak to widać na grafiku poniżej, po lewej stronie.

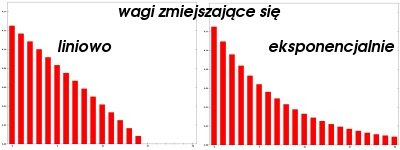
Okazuje się że w analizie technicznej, jak majstrowanie przy grafikach się szumnie nazywa, praktyczne jest czasem jeszcze wydatniejsze uprzywilejowanie najświeższych wartości, przy jednoczesnym wytłumieniu wpływu jaki na naszą średnią mają wartości starsze. Można to elegancko osiągnąć poprzez wagi wykładniczo opadające, takie jak po prawej stronie w grafiku powyżej. Utworzona w ten sposób ważona średnia krocząca nosi nazwę EMA – exponential moving average.

EMA to zatem WMA bardziej agresywnie ważona. Czytelnik domyśli się od razu że EMA wprowadza nowe możliwości komplikacji w zasadzie prostego pomysłu. Dzieje się tak ponieważ metod wykładniczego przytłumiania elementów średniej może być kilka. I rzeczywiście, istnieją różne warianty EMA. Aby jednak wynagrodzić drogiego czytelnika który aż tu dotarł w tym wpisie damy sobie na razie spokój z szerszą dyskusją tych wariantów, przechodząc od razu do końcowego wzorku.

EMAdziś = EMAwczoraj + alfa * (cena – EMAwczoraj)

gdzie alfa = 2/(n+1) jest tzw. współczynnikiem wygładzania, zależnym od zakresu naszej średniej. Przykładowo, dla dwunastodniowej EMA(12) współczynnik wygładzania alfa wyniesie 0.15.

Formułka [4] pozwala nam prosto znaleźć nową wartość EMA, na podstawie poprzedniej wartości EMA i nowej ceny. Współczynnik alfa jest dla danej EMA stały.

Grafik poniżej ilustruje różnicę między MA i EMA na praktycznym przykładzie nieśmiertelnego srebra. Tym razem widzimy na nim dwie średnie kroczące, obie o jednakowym zakresie 50 dni. Linia niebieska to zwykła nieważona MA(50), zaś linia czerwona reprezentuje eksponencjalną średnią kroczącą EMA(50).

Tak jak wspomnieliśmy wcześniej, MA(50) jest z definicji jest dosyć powolna, by nie powiedzieć „mułowata”, i z dużym opóźnieniem reaguje na ruchy cen waloru. W porównaniu do niej czerwona EMA(50) to Ferrari, znacznie szybciej i ostrzej reagująca na te zmiany. W szczególności EMA(50) lepiej oddaje charakter zmian ceny srebra w postaci wyraźnej, wznoszącej się „piły”.

Chętni na dalsze szperanie we wzorkach i zgłębianie średnich kroczących mogą zajrzeć do wikipedii.

p.s. Więcej o srebrze, złocie i szczegółach inwestowania w metale szlachetne dla abonentów naszego cyrkularza emalowego DwaGrosze NewsLetter. Dołącz i Ty.